Geometrie in der 8. Klasse meistern
Wie löst man eigentlich knifflige Geometrieaufgaben in der 8. Klasse? Geometrie kann eine Herausforderung sein, aber mit den richtigen Werkzeugen und Strategien ist sie zu meistern. Dieser Artikel bietet einen umfassenden Leitfaden, um geometrische Probleme der Mittelstufe erfolgreich zu bewältigen.
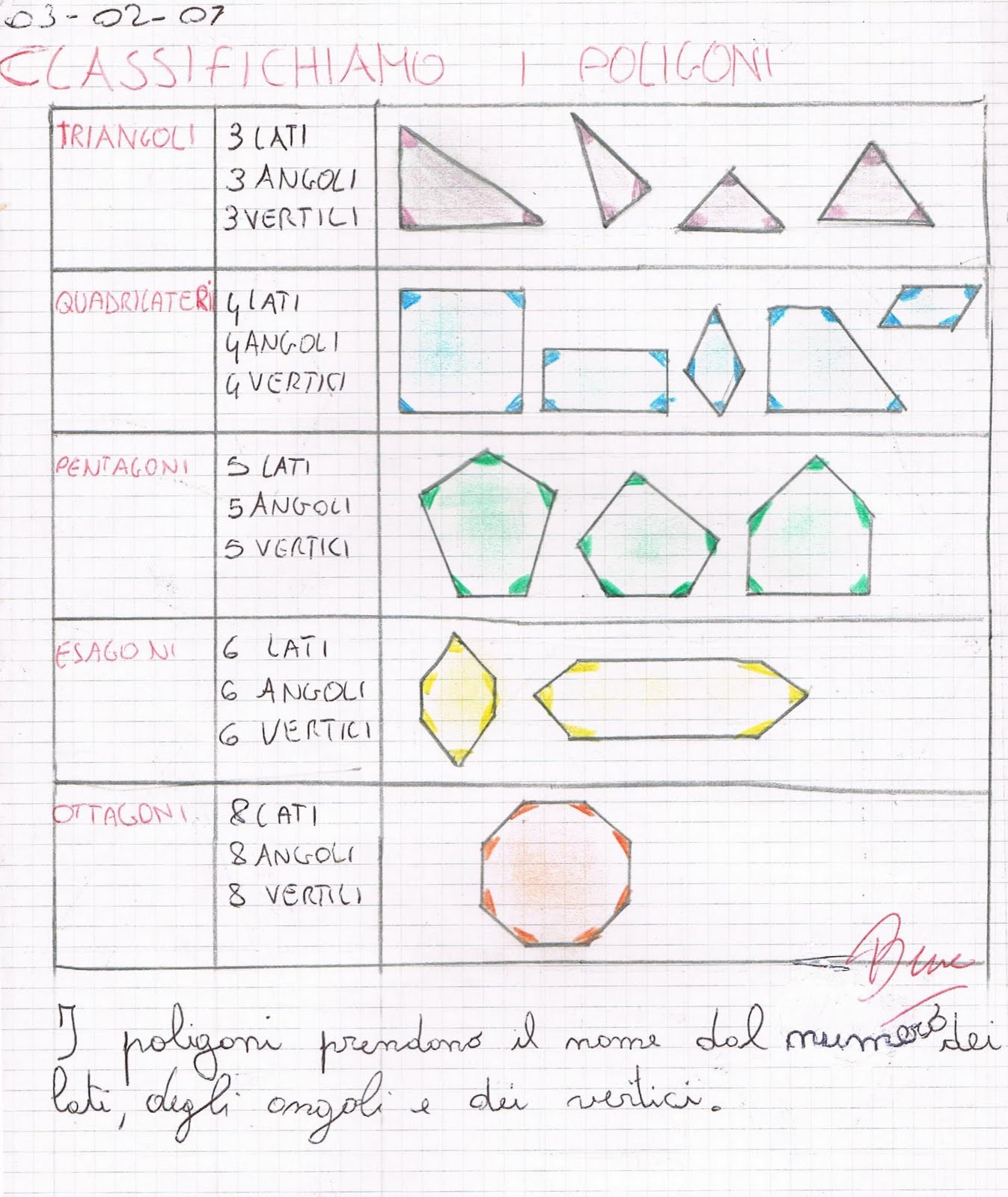
Die 8. Klasse ist oft der Zeitpunkt, an dem die Geometrie komplexer wird. Von der Berechnung von Flächen und Volumen bis hin zur Anwendung des Satzes von Pythagoras – die Anforderungen steigen. Dieser Artikel hilft Schülern, die Grundlagen zu verstehen und ihre Fähigkeiten im Lösen geometrischer Probleme zu verbessern.
„Risolvi problemi di geometria terza media“ – so lautet die italienische Bezeichnung für das Lösen von Geometrieaufgaben in der 8. Klasse. Dieser Artikel konzentriert sich auf genau dieses Thema und bietet praktische Hilfestellungen für Schüler, Eltern und Lehrer.
Von der Flächenberechnung von Dreiecken und Vierecken über das Verständnis von Winkelbeziehungen bis hin zur Berechnung des Volumens von Prismen und Zylindern: Dieser Artikel deckt ein breites Spektrum an Themen ab. Erfahren Sie, wie Sie Schritt für Schritt komplexe Probleme angehen und erfolgreich lösen können.
Geometrie ist nicht nur ein abstraktes Schul-Thema, sondern hat auch praktische Relevanz in vielen Bereichen des Lebens. Von der Architektur und dem Ingenieurwesen bis hin zur Kunst und dem Design – geometrische Prinzipien sind überall zu finden. Dieser Artikel verdeutlicht die Bedeutung der Geometrie und motiviert Schüler, sich aktiv mit ihr auseinanderzusetzen.
Die Geschichte der Geometrie reicht Jahrtausende zurück. Bereits im alten Ägypten und Babylonien wurden geometrische Kenntnisse für die Landvermessung und den Bau von Pyramiden und Tempeln verwendet. Die Griechen entwickelten die Geometrie dann zu einer deduktiven Wissenschaft. Euklids „Elemente“ gelten als grundlegendes Werk der Geometrie und haben bis heute Einfluss auf die Mathematik.
Ein typisches Problem in der 8. Klasse ist die Berechnung des Volumens eines Zylinders. Die Formel dafür lautet: V = πr²h, wobei r der Radius der Grundfläche und h die Höhe des Zylinders ist. Beispiel: Ein Zylinder hat einen Radius von 5 cm und eine Höhe von 10 cm. Das Volumen beträgt V = π * 5² * 10 ≈ 785,4 cm³.
Vorteile der Geometriekenntnisse
Geometrie fördert das logische Denken, das räumliche Vorstellungsvermögen und die Problemlösekompetenz.
Schritt-für-Schritt-Anleitung zur Lösung von Geometrieaufgaben
1. Lesen Sie die Aufgabenstellung sorgfältig. 2. Zeichnen Sie eine Skizze. 3. Identifizieren Sie die gegebenen Größen. 4. Bestimmen Sie die gesuchten Größen. 5. Wählen Sie die passende Formel. 6. Setzen Sie die Werte ein. 7. Berechnen Sie das Ergebnis. 8. Überprüfen Sie Ihre Lösung.
Häufig gestellte Fragen (FAQs)
1. Wie berechnet man den Flächeninhalt eines Dreiecks? A = 0,5 * g * h
2. Was ist der Satz des Pythagoras? a² + b² = c²
3. Wie berechnet man den Umfang eines Kreises? U = 2πr
4. Was ist ein rechtwinkliges Dreieck? Ein Dreieck mit einem 90°-Winkel.
5. Wie berechnet man das Volumen eines Würfels? V = a³
6. Was ist ein Parallelogramm? Ein Viereck mit zwei Paaren paralleler Seiten.
7. Wie berechnet man den Flächeninhalt eines Trapezes? A = 0,5 * (a + c) * h
8. Was ist ein Kreisbogen? Ein Teil des Kreisumfangs.Tipps und Tricks
Nutzen Sie Skizzen und Zeichnungen, um die Aufgaben besser zu visualisieren. Formeln auf Karteikarten schreiben und regelmäßig wiederholen. Übungsaufgaben lösen und die Lösungen überprüfen.
Zusammenfassend lässt sich sagen, dass das Lösen von Geometrieaufgaben in der 8. Klasse eine wichtige Fähigkeit ist, die logisches Denken, räumliches Vorstellungsvermögen und Problemlösekompetenz fördert. Die Beherrschung der grundlegenden Konzepte und Formeln ist entscheidend für den Erfolg in der Geometrie. Durch Übung, das Anwenden von Strategien und das Verständnis der zugrundeliegenden Prinzipien können Schüler ihre Fähigkeiten verbessern und die Herausforderungen der Geometrie meistern. Nutzen Sie die in diesem Artikel vorgestellten Tipps und Tricks, um Ihre Geometriekenntnisse zu vertiefen und Ihre Noten zu verbessern. Investieren Sie Zeit und Mühe in das Lernen von Geometrie – es wird sich langfristig auszahlen!
Konrad zimmermann arzt informationen und expertise
Perfekte spruche zum 40 geburtstag fur frauen entdecken
Evangelische gemeinde in feldkirchen altwied entdecken