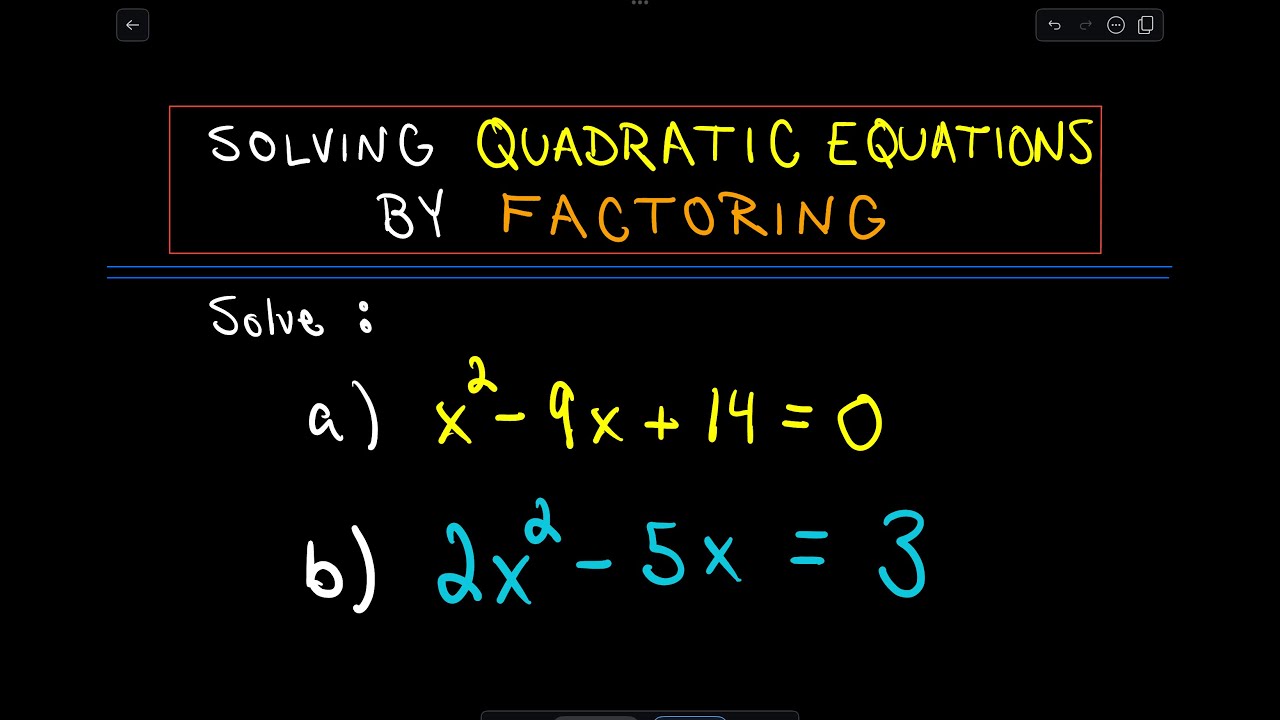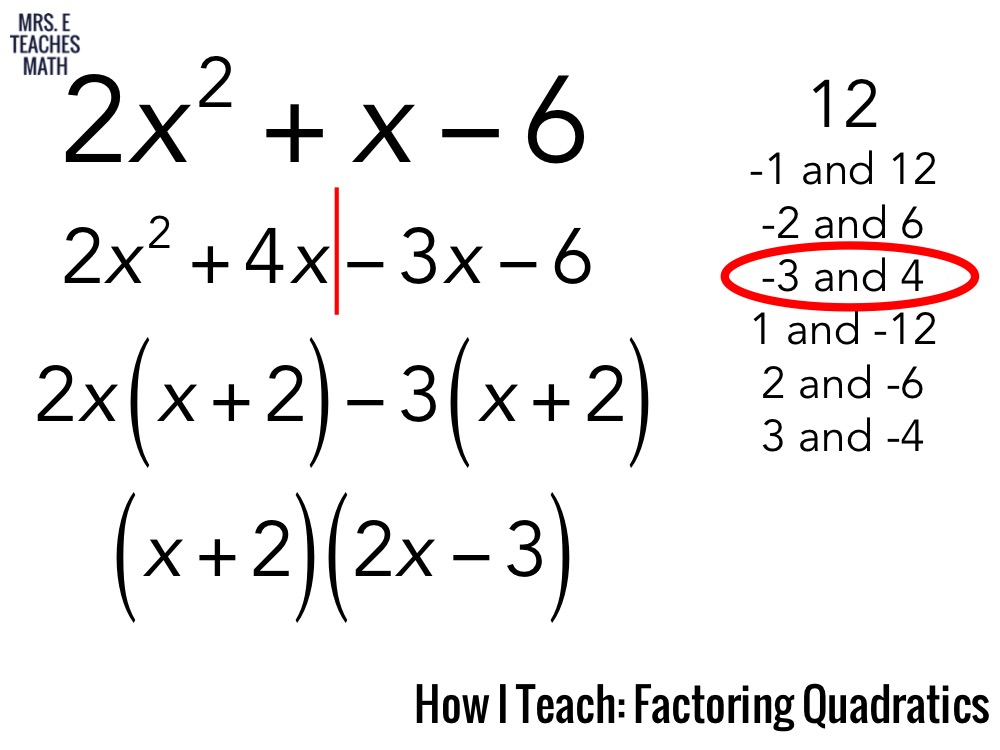Résoudre des équations du second degré par factorisation
Comment résoudre l'équation 4x² + 9x - 9 = 0 ? La factorisation est une méthode puissante et élégante pour trouver les solutions. Découvrons ensemble comment utiliser cette technique pour décoder les mystères des équations du second degré.
La résolution d'équations est un pilier des mathématiques. Que ce soit pour calculer des trajectoires, optimiser des ressources ou modéliser des phénomènes physiques, la capacité à trouver les valeurs inconnues d'une équation est essentielle. Parmi les équations les plus courantes, on retrouve les équations du second degré, de la forme ax² + bx + c = 0. La factorisation offre une approche efficace pour résoudre ces équations, notamment l'équation 4x² + 9x - 9 = 0.
L'histoire de la factorisation remonte à l'Antiquité, avec des traces de son utilisation chez les Babyloniens et les Grecs. Au fil des siècles, cette technique s'est affinée et est devenue un outil fondamental en algèbre. La factorisation permet de décomposer une expression complexe en un produit de facteurs plus simples, facilitant ainsi la résolution d'équations et la simplification d'expressions mathématiques. Dans le cas de 4x² + 9x - 9 = 0, la factorisation nous aidera à trouver les valeurs de x qui satisfont l'équation.
Comprendre la factorisation est crucial pour tout étudiant en mathématiques. Cette méthode offre une alternative à la formule quadratique et permet de développer une meilleure intuition algébrique. Maîtriser la factorisation, c'est acquérir un outil puissant pour résoudre des problèmes mathématiques plus complexes. Prenons l'exemple de 4x² + 9x - 9 = 0. En factorisant cette équation, nous pourrons identifier les racines, c'est-à-dire les valeurs de x qui rendent l'équation vraie.
Dans le cas précis de 4x² + 9x - 9 = 0, la factorisation peut être un peu plus complexe qu'avec des coefficients plus simples. Il faut trouver deux nombres dont le produit est égal à 4*(-9) = -36 et dont la somme est égale à 9. Après quelques essais, on trouve 12 et -3. On réécrit alors l'équation sous la forme 4x² + 12x - 3x - 9 = 0. En factorisant par groupes, on obtient 4x(x+3) - 3(x+3) = 0, puis (4x-3)(x+3) = 0. Les solutions sont donc x = 3/4 et x = -3.
Résoudre une équation du second degré par factorisation revient à transformer l'équation en un produit de facteurs égal à zéro. Par exemple, si (ax + b)(cx + d) = 0, alors soit ax + b = 0, soit cx + d = 0.
Avantages de la factorisation:
1. Simplicité : La factorisation peut être plus rapide et plus intuitive que la formule quadratique, surtout pour les équations avec des coefficients entiers.
2. Développement de l'intuition : La factorisation permet de mieux comprendre la structure des équations et les relations entre les coefficients.
3. Applications : La factorisation est utilisée dans de nombreux domaines des mathématiques et des sciences.
Questions fréquemment posées :
1. Quand puis-je utiliser la factorisation ? La factorisation est particulièrement efficace pour les équations du second degré dont les racines sont des nombres rationnels.
2. La factorisation est-elle toujours possible ? Non, certaines équations du second degré ne peuvent pas être factorisées facilement.
3. Existe-t-il d'autres méthodes pour résoudre les équations du second degré ? Oui, la formule quadratique permet de résoudre toutes les équations du second degré.
4. Comment vérifier mes solutions ? En remplaçant les valeurs de x trouvées dans l'équation originale.
5. La factorisation est-elle utile pour les équations de degré supérieur ? Oui, mais elle devient plus complexe à mettre en œuvre.
6. Quels sont les pièges à éviter lors de la factorisation ? Faire attention aux signes et bien vérifier les facteurs trouvés.
7. Où puis-je trouver plus d'exercices sur la factorisation ? De nombreux sites web et manuels scolaires proposent des exercices corrigés.
8. La factorisation est-elle la méthode la plus rapide ? Cela dépend de l'équation. Parfois, la formule quadratique peut être plus rapide.
En conclusion, la factorisation est une méthode puissante et élégante pour résoudre des équations du second degré comme 4x² + 9x - 9 = 0. Elle permet de développer une meilleure compréhension des équations et offre une alternative efficace à la formule quadratique. Bien que certaines équations puissent être difficiles à factoriser, la maîtrise de cette technique est un atout précieux pour tout étudiant en mathématiques. N'hésitez pas à pratiquer la factorisation avec différents exemples pour renforcer vos compétences et explorer les subtilités de cette méthode essentielle.
Devinez le jeu de societe le defi ultime pour les experts en jeux
Gohan et lultra instinct mythe ou realite
Gta vice city retro gaming resolution 640x480 sur windows 10