De Turing Machine voor L a^n b^n c^(n+1) Ontdecoded
Stel je een machine voor, een theoretische machine, die de basis vormt voor alle moderne computers. Een machine die elk denkbaar algoritme kan uitvoeren. Dit is de Turing Machine, een concept bedacht door Alan Turing. Maar hoe werkt zo'n machine voor een specifieke taal, zoals L = {a^n b^n c^(n+1) | n >= 0}?
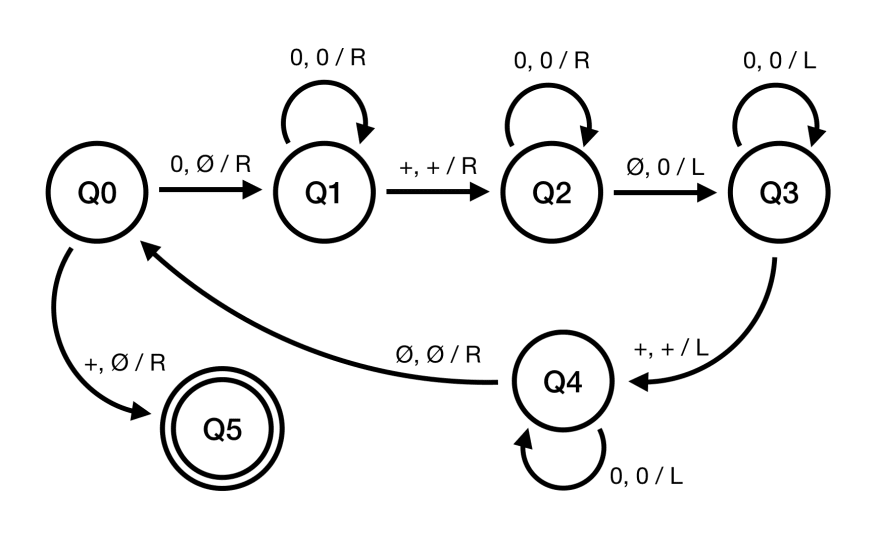
De taal L = {a^n b^n c^(n+1) | n >= 0} beschrijft strings met een specifieke structuur: 'n' aantal 'a's, gevolgd door 'n' aantal 'b's, en tenslotte 'n+1' aantal 'c's. Een Turing Machine voor deze taal moet dus in staat zijn om deze structuur te herkennen en te valideren. Maar hoe ontwerp je zo'n machine?
Het ontwerpen van een Turing Machine voor L = {a^n b^n c^(n+1)} is een complexe, maar fascinerende uitdaging. Het vereist een diepgaand begrip van de werking van Turing Machines en de logica erachter. Deze machines opereren op een tape met symbolen en bewegen zich stap voor stap door de tape, lezend en schrijvend, gebaseerd op een set regels.
De complexiteit van de taal L = {a^n b^n c^(n+1)} komt voort uit de afhankelijkheid tussen het aantal 'a's, 'b's en 'c's. De Turing Machine moet bijhouden hoeveel 'a's en 'b's er zijn om te controleren of het aantal 'c's correct is. Dit vereist een slimme manipulatie van de symbolen op de tape en een zorgvuldige planning van de stappen die de machine moet nemen.
In deze verkenning van Turing Machines voor L = {a^n b^n c^(n+1)}, zullen we de werking van zo'n machine ontrafelen. We zullen de stappen doorlopen die nodig zijn om de taal te herkennen en de uitdagingen bespreken die zich voordoen bij het ontwerpen van een dergelijke machine. Bereid je voor op een reis door de theoretische wereld van berekenbaarheid.
Alan Turing introduceerde de Turing Machine in 1936 als een abstract model van berekening. De machine, hoewel theoretisch, kan elk berekenbaar probleem oplossen. Het ontwerpen van een Turing Machine voor L = {a^n b^n c^(n+1)} illustreert de kracht en complexiteit van dit model. Het laat zien hoe een eenvoudige machine, met een beperkte set instructies, complexe patronen en relaties kan herkennen.
Een mogelijke implementatie zou gebruik maken van markeringen op de tape om bij te houden welke 'a', 'b' en 'c' al gecontroleerd zijn. De machine zou eerst een 'a' markeren en dan naar rechts bewegen tot een 'b' gevonden wordt, die ook gemarkeerd wordt. Vervolgens zoekt de machine een 'c' en markeert deze. Dit proces herhaalt zich tot alle 'a's en 'b's gemarkeerd zijn. Tenslotte controleert de machine of er precies één ongemarkeerde 'c' overblijft.
Helaas, vanwege de complexiteit en de theoretische aard van dit onderwerp, zijn concrete voorbeelden, checklists en stap-voor-stap handleidingen moeilijk te presenteren in een algemeen begrijpelijke vorm. Diepgaande kennis van formele talen en automatentheorie is vereist voor een volledige begrip.
Voor- en nadelen van een Turing Machine voor L = {a^n b^n c^(n+1)}
Het is belangrijk te onthouden dat de Turing Machine een theoretisch model is. Praktische implementaties voor specifieke talen zoals L = {a^n b^n c^(n+1)} zijn complex en niet direct toepasbaar in real-world scenarios. De waarde ligt in het theoretische begrip van berekenbaarheid.
Veelgestelde vragen:
1. Wat is een Turing Machine? Een Turing Machine is een theoretisch model van berekening.
2. Wat is L = {a^n b^n c^(n+1)}? Het is een formele taal die strings beschrijft met een specifieke structuur.
3. Waarom is dit relevant? Het helpt ons de grenzen van berekenbaarheid te begrijpen.
4. Hoe complex is het om zo'n machine te ontwerpen? Het is een complexe taak die diepgaande kennis vereist.
5. Zijn er praktische toepassingen? De waarde ligt vooral in het theoretische begrip.
6. Wat zijn de beperkingen? Het is een theoretisch model, geen praktische tool.
7. Waar kan ik meer leren? Boeken over automatentheorie en formele talen zijn een goede start.
8. Hoe relateert dit aan moderne computers? De Turing Machine vormt de theoretische basis voor alle moderne computers.
De Turing Machine voor L = {a^n b^n c^(n+1)} biedt een fascinerend inzicht in de kracht en complexiteit van berekenbaarheid. Hoewel de praktische implementatie uitdagend is, is het theoretische begrip van groot belang voor computerwetenschappers en iedereen die geïnteresseerd is in de fundamentele principes van berekening. Door de werking van deze machine te bestuderen, kunnen we de grenzen van wat berekenbaar is beter begrijpen en de fundamenten van de moderne computerwetenschap waarderen. De Turing Machine blijft een essentieel concept voor het begrijpen van de mogelijkheden en beperkingen van computers en algoritmen. Het is een bewijs van de genialiteit van Alan Turing en een blijvende bijdrage aan ons begrip van de wereld van berekening.
Draaitabellen maandveld toevoegen slim gebruiken
Je hebt gelijk de kracht van erkenning
Fietsen op de fiets ontdek de vrijheid van twee wielen