Geheim van de Gelijkbenige Driehoek Ontdek de Magie
Heb je je ooit afgevraagd waarom sommige driehoeken er zo perfect symmetrisch uitzien? Dat komt door de magische eigenschappen van een gelijkbenige driehoek! Deze bijzondere geometrische figuren hebben al eeuwenlang wiskundigen en kunstenaars geïnspireerd. Laten we samen duiken in de wondere wereld van de gelijkbenige driehoek en de geheimen ervan ontrafelen.
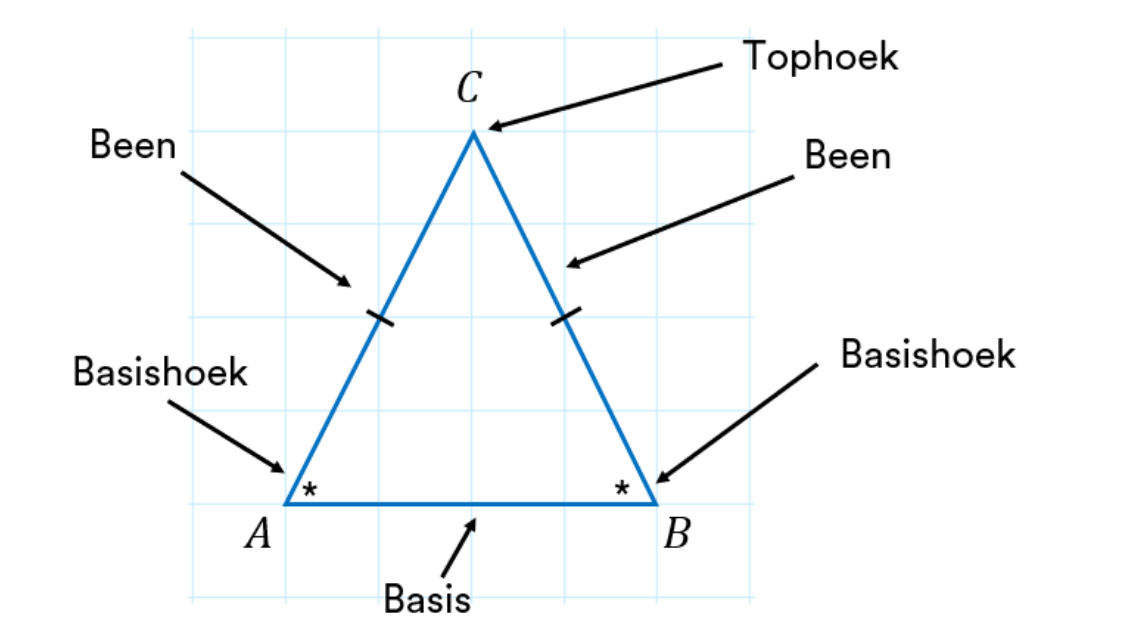
Een gelijkbenige driehoek is een driehoek met twee gelijke zijden. Deze gelijke zijden worden de benen genoemd. De derde zijde wordt de basis genoemd. Door de gelijke benen ontstaan er ook twee gelijke hoeken, de basishoeken. Deze unieke kenmerken geven de gelijkbenige driehoek een elegante symmetrie en leiden tot interessante wiskundige relaties.
Al in de oudheid speelden gelijkbenige driehoeken een belangrijke rol. Denk maar aan de piramides van Egypte, waarvan de zijvlakken vaak gelijkbenige driehoeken vormen. Ook in de architectuur en kunst komen we deze driehoeken veelvuldig tegen. Het begrijpen van de eigenschappen van een gelijkbenige driehoek is essentieel voor iedereen die zich bezighoudt met wiskunde, design of techniek.
Maar wat zijn nu precies die eigenschappen? Naast de gelijke benen en basishoeken, heeft een gelijkbenige driehoek nog andere bijzondere kenmerken. Zo deelt de hoogtelijn vanuit de tophoek de basis precies middendoor. Deze hoogtelijn is tegelijkertijd de bissectrice van de tophoek en de middenloodlijn van de basis. Deze eigenschappen maken de gelijkbenige driehoek een fascinerend object voor geometrische analyses.
Het leren over gelijkbenige driehoeken is niet alleen nuttig, maar ook leuk! Door te experimenteren met verschillende vormen en maten, kun je zelf de eigenschappen ontdekken en de symmetrie bewonderen. Of je nu een student bent die zijn wiskundekennis wil verbeteren, of gewoon geïnteresseerd bent in geometrie, de gelijkbenige driehoek heeft voor ieder wat wils.
De gelijkbenige driehoek is al sinds de oudheid bekend, en speelt een rol in de Euclidische meetkunde. Een belangrijk probleem gerelateerd aan de eigenschappen van gelijkbenige driehoeken is het bewijzen van stellingen met betrekking tot de basishoeken en de hoogtelijn.
Voorbeeld: Een driehoek ABC met AB = AC = 5 cm en BC = 6 cm is een gelijkbenige driehoek. De hoeken bij B en C zijn gelijk.
Voordelen van het begrijpen van de eigenschappen van een gelijkbenige driehoek:
1. Oplossen van geometrische problemen: Kennis van de eigenschappen helpt bij het berekenen van hoeken, zijden en oppervlaktes.
2. Toepassingen in de praktijk: Van architectuur tot engineering, de eigenschappen van gelijkbenige driehoeken worden in diverse disciplines gebruikt.
3. Versterken van wiskundig inzicht: Het bestuderen van gelijkbenige driehoeken verdiept het begrip van geometrie en symmetrie.
Veelgestelde vragen:
1. Wat is een gelijkbenige driehoek? Een driehoek met twee gelijke zijden.
2. Wat zijn de basishoeken? De twee gelijke hoeken aan de basis.
3. Wat is de tophoek? De hoek tussen de twee gelijke zijden.
4. Wat is de hoogtelijn? De lijn loodrecht op de basis vanuit de tophoek.
5. Wat is de bissectrice? De lijn die een hoek in twee gelijke delen deelt.
6. Wat is de middenloodlijn? De lijn loodrecht op een lijnstuk door het middenpunt.
7. Hoe bereken je de oppervlakte van een gelijkbenige driehoek? (basis * hoogte) / 2.
8. Hoe bewijs je dat een driehoek gelijkbenig is? Door aan te tonen dat twee zijden gelijk zijn of twee hoeken gelijk zijn.
Tips en trucs: Teken altijd een schets van de driehoek. Label de zijden en hoeken. Gebruik de stellingen over gelijkbenige driehoeken om onbekende waarden te berekenen.
Conclusie: De gelijkbenige driehoek is een fascinerende geometrische figuur met unieke eigenschappen. Van de symmetrie tot de wiskundige relaties, de gelijkbenige driehoek biedt een rijke bron van kennis en inspiratie. Door de eigenschappen te begrijpen, kunnen we geometrische problemen oplossen, praktische toepassingen ontdekken en ons wiskundig inzicht versterken. Duik in de wereld van de gelijkbenige driehoek en ontdek de magie ervan! Of je nu een student, een professional of gewoon een nieuwsgierige geest bent, de gelijkbenige driehoek heeft iets te bieden voor iedereen. Verken de symmetrie, de formules en de toepassingen, en laat je verrassen door de elegantie en de kracht van deze bijzondere driehoek. Begin vandaag nog met het verkennen van de fascinerende wereld van de gelijkbenige driehoek!
Tijdmanagement werkbladen jouw geheime wapen voor productiviteit
Duivenhokken te koop vind jouw ideale duivenhok
Ontdek de magie van weerradar technologie



_original.png)