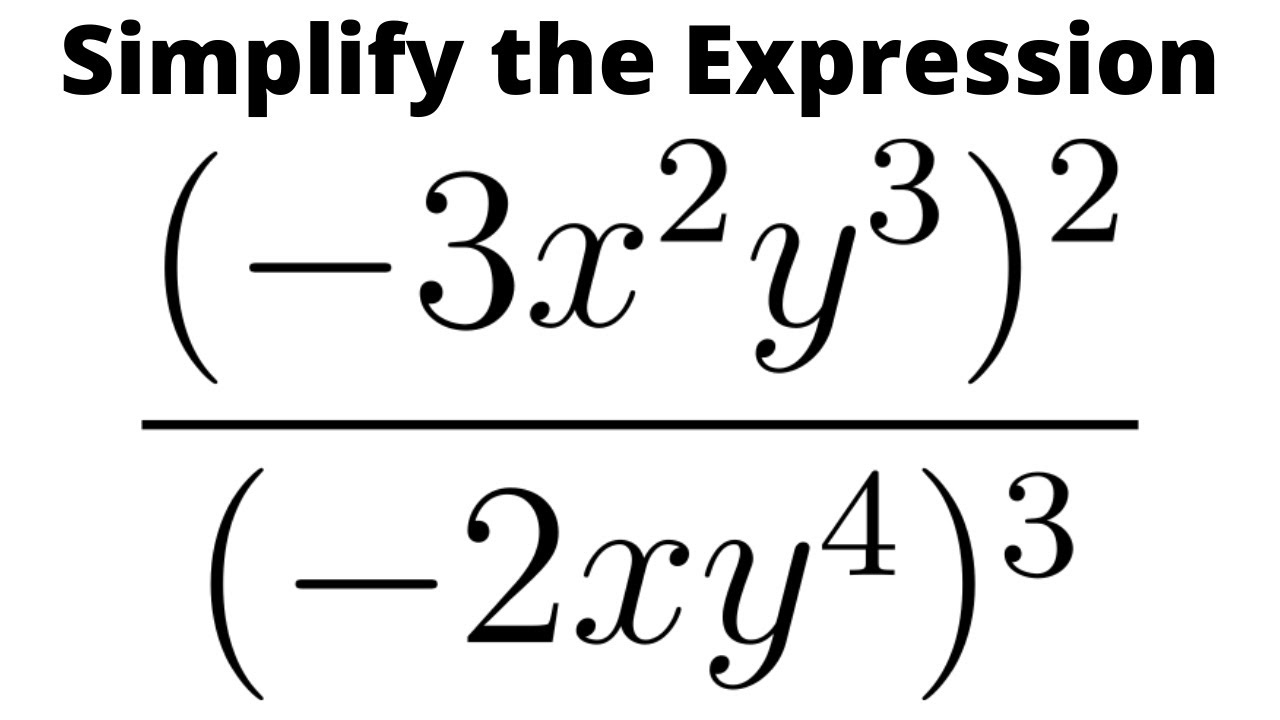Vereenvoudig Algebra -2x 3y xy 2
Hoe navigeer je door de wondere wereld van algebra? Het kan soms voelen als een jungle van x'en, y's en getallen, maar met de juiste tools hoef je niet te verdwalen. Laten we ons concentreren op het vereenvoudigen van uitdrukkingen zoals -2x 3y xy 2. Het lijkt misschien ingewikkeld, maar het is eigenlijk een fluitje van een cent als je de basisregels kent.
Stel je voor dat je een recept hebt met verschillende ingrediënten. Je kunt die ingrediënten groeperen en combineren om het recept overzichtelijker te maken. Dat is precies wat we doen met algebraïsche uitdrukkingen. We combineren gelijke termen om de uitdrukking te vereenvoudigen.
De uitdrukking -2x 3y xy 2 bevat variabelen (x en y) en coëfficiënten (-2, 3 en 2, hoewel de 1 voor xy impliciet is). Om deze uitdrukking te vereenvoudigen, moeten we de termen met dezelfde variabelen combineren. Dit proces is fundamenteel voor het oplossen van complexere algebraïsche problemen.
Het vereenvoudigen van algebraïsche uitdrukkingen is als het opruimen van je kamer. Je groepeert sokken bij sokken, shirts bij shirts en boeken bij boeken. In algebra groeperen we x'en bij x'en, y's bij y's, en zo verder. Dit maakt het niet alleen netter, maar ook veel gemakkelijker om mee te werken.
De uitdrukking -2x 3y xy 2 kan herschreven worden als -2x + 3y + xy + 2. Omdat er geen gelijke termen zijn (geen termen met dezelfde variabelen en exponenten), is dit de meest vereenvoudigde vorm. Het is alsof je appels, sinaasappels en bananen hebt - je kunt ze niet combineren tot één fruitsoort.
De geschiedenis van algebra gaat terug tot eeuwen geleden, met wortels in het oude Babylonië en Egypte. Het vereenvoudigen van uitdrukkingen is een essentieel onderdeel van deze geschiedenis en vormt de basis voor veel wiskundige concepten.
Voorbeeld: Vereenvoudig 2x + 3y - x + 5y. Combineer de x-termen: 2x - x = x. Combineer de y-termen: 3y + 5y = 8y. De vereenvoudigde uitdrukking is x + 8y.
Voordelen van vereenvoudigen:
1. Overzichtelijkheid: Complexe uitdrukkingen worden gemakkelijker te begrijpen.
2. Efficiëntie: Het bespaart tijd bij het oplossen van vergelijkingen.
3. Nauwkeurigheid: Het vermindert de kans op fouten.
Stap-voor-stap handleiding:
1. Identificeer gelijke termen.
2. Combineer de coëfficiënten van gelijke termen.
3. Schrijf de vereenvoudigde uitdrukking.
Veelgestelde vragen:
1. Wat is een term in algebra? Antwoord: Een term is een getal, een variabele of een product van getallen en variabelen.
2. Wat is een coëfficiënt? Antwoord: Een coëfficiënt is het getal voor een variabele.
3. Hoe combineer ik gelijke termen? Antwoord: Tel of trek de coëfficiënten van gelijke termen op.
4. Kan ik x en x² combineren? Antwoord: Nee, dit zijn geen gelijke termen.
5. Wat als er geen gelijke termen zijn? Antwoord: Dan is de uitdrukking al vereenvoudigd.
6. Waarom is vereenvoudigen belangrijk? Antwoord: Het maakt complexere berekeningen mogelijk.
7. Waar kan ik meer over algebra leren? Antwoord: Online bronnen en leerboeken bieden uitgebreide informatie.
8. Hoe oefen ik het vereenvoudigen van uitdrukkingen? Antwoord: Werk veel oefenopgaven!
Tips en trucs: Gebruik kleuren om gelijke termen te markeren. Schrijf elke stap netjes op om fouten te voorkomen.
Kortom, het vereenvoudigen van algebraïsche uitdrukkingen zoals -2x 3y xy 2 is een essentiële vaardigheid. Het legt de basis voor complexere algebra en wiskunde. Door gelijke termen te combineren, maken we uitdrukkingen overzichtelijker, efficiënter en minder foutgevoelig. Oefening baart kunst, dus begin vandaag nog met het vereenvoudigen van je eigen algebraïsche uitdrukkingen! Het begrijpen van deze basisprincipes opent de deur naar een dieper begrip van wiskunde en stelt je in staat om complexere problemen met vertrouwen aan te pakken. Dus, pak je pen en papier, en begin met oefenen! Je zult versteld staan hoe snel je een expert wordt in het vereenvoudigen van zelfs de meest ingewikkelde algebraïsche uitdrukkingen.
Draaitabellen je data ontrafelen rocken
Nba games op tv vandaag beleef de spanning live
Het mysterieuze leven van een octopus ontrafeld